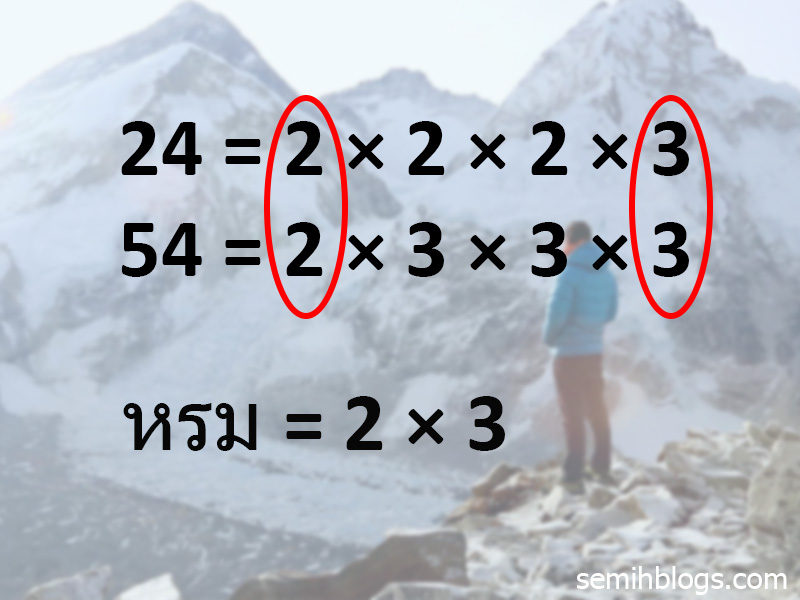ตัวหารร่วมมาก หรือ ห.ร.ม. คือตัวเลขจำนวนเต็มบวกที่มีค่ามากที่สุด ที่สามารถหารตัวเลขตั้งแต่สองตัวขึ้นไป และตัวเลขเหล่านั้นต้องไม่เป็น 0 ทั้งหมด ยกตัวอย่าง เช่น หรม ของ 8 และ 12 คือ 4 เพราะ 4 เป็นตัวเลขที่มากที่สุดที่หารทั้ง 8 และ 12 ลงตัว ประโยชน์ของ หรม นั้นมักจะใช้ในการลดทอนเศษส่วนให้เป็นเศษส่วนอย่างต่ำ
การหาค่าของ หรม นั้นสามารถทำได้หลายวิธี สำหรับวันนี้เราจะมาแนะนำวิธีการหา หรม โดยวิธีการแยกตัวประกอบ ซึ่งเป็นวิธีที่ง่ายและทำได้อย่างรวดเร็ว มาดูตัวอย่างการแยก
ขั้นตอนการหา ห.ร.ม.โดยวิธีแยกตัวประกอบ
ในการหา หรม ด้วยมีธีการแยกตัวประกอบ จะมีขั้นตอนอยู่ทั้งหมด 3 ขั้นตอนง่ายๆ คือ
1) แยกตัวประกอบของตัวเลขแต่กละตัวออกมา
2) หาตัวประกอบร่วมของตัวเลขทั้งหมด
3) นำตัวประกอบร่วมกันมาคูณกันเพื่อหาค่า หรม
ตัวอย่างที่ 1 จงหา หรม ของ 24 และ 54 (แบบละเอียด)
ขั้นตอนแรก นำตัวเลขทั้งสองตัวมาแยกตัวประกอบก่อน
แยกตัวประกอบของ 24 ด้วยการหาจำนวนเฉพาะที่น้อยที่สุด ที่สามารถหาร 24 ลงตัว นั่นคือ 2 ดังนั้นเราแยกออกได้เป็น
24 = 2 × 12
สังเกตว่า 12 ยังไม่ใช่จำนวนเฉพาะ ดังนั้นนำ 12 มาแยกตัวประกอบต่อ โดยจำนวนเฉพาะที่น้อยที่สุดที่สามารถหาร 12 ลงตัวคือ 2 ดังนั้นเราแยกออกได้เป็น
24 = 2 × 2 × 6
สังเกตว่า 6 ยังไม่ใช่จำนวนเฉพาะเช่นเดิม ดังนั้นเรานำ 6 มาแยกตัวประกอบต่อ โดยจำนวนเฉพาะที่น้อยที่สุดที่สามารถหาร 6 ลงตัวคือ 2 ดังนั้นเราแยกออกได้เป็น
24 = 2 × 2 × 2 × 3
สังเกตว่า ในตอนนี้ตัวเลขทุกตัวที่เราแยกออกมาเป็นจำนวนเฉพาะหมดแล้ว
ดังนั้นตัวประกอบของ 24 คือ 2 × 2 × 2 × 3
ต่อไปแยกตัวประกอบของ 54 กันต่อ จำนวนเฉพาะที่น้อยที่สุดที่หาร 54 ลงตัวคือ 2 ดังนั้นจะได้
54 = 2 x 27
สังเกตว่า 27 ยังไม่ใช่จำนวนเฉพาะ นำมาแยกต่อ และจำนวนเฉพาะที่น้อยที่สุดที่หาร 27 ลงตัวคือ 3 ดังนั้นจะได้
54 = 2 x 3 x 9
เช่นเดิม 9 ยังไม่ใช่จำนวนเฉพาะนำมาแยกต่อ และจำนวนเฉพาะที่น้อยที่สุดที่หาร 9 ลงตัวคือ 3 ดังนั้นจะได้
54 = 2 x 3 x 3 x 3
ในตอนนี้ สังเกตว่าตัวประกอบทุกตัวเป็นจำนวนเฉพาะแล้ว
ดังนั้นตัวประกอบของ 24 คือ 2 x 3 x 3 x 3
ดังนั้นในขั้นตอนแรกตัวประกอบของ 24 และ 54 คือ
24 = 2 x 3 x 3 x 3
54 = 2 x 3 x 3 x 3
ขั้นตอนที่สอง หาตัวประกอบร่วมของตัวเลขทั้งสองว่ามีอะไรบ้าง
24 = 2 × 2 × 2 × 3
54 = 2 x 3 x 3 x 3
ขั้นตอนที่สาม นำตัวประกอบร่วมมาคูณกันเพื่อหาค่า หรม
2 x 3 = 6
ดังนั้น หรม ของ 24 และ 54 คือ 6

ตัวอย่างที่ 2 จงหา หรม ของ 8 และ 12
ขั้นตอนแรก ตัวอย่างที่สองนี้จะข้ามการแยกตัวประกอบแบบละเอียดไป และเมื่อเรานำ 8 และ 12 มาแยกตัวประกอบจะได้
8 = 2 x 2 x 2
12 = 2 x 2 x 3
ขั้นตอนที่สอง หาตัวประกอบร่วมของตัวเลขทั้งสองว่ามีอะไรบ้าง
8 = 2 x 2 x 2
12 = 2 x 2 x 3
ขั้นตอนที่สาม นำตัวประกอบร่วมมาคูณกันเพื่อหาค่า หรม
2 x 2 = 4
ดังนั้น หรม ของ 8 และ 12 คือ 4

ตัวอย่างที่ 3 จงหา หรม ของ 12, 15 และ 30
ต่อไปมาดูตัวอย่างการหา หรม ของตัวเลข 3 ตัวกันบ้าง ซึ่งหลักการก็เหมือนเดิม แยกตัวประกอบของตัวเลขแต่ละตัวออกมา
ขั้นตอนแรก แยกตัวประกอบของของ 12, 15 และ 30 จะได้ดังนี้
12 = 2 x 2 x 3
15 = 3 x 5
30 = 2 x 3 x 5
ขั้นตอนที่สอง จับคู่ตัวประกอบร่วมของตัวเลขทั้งสามตัวจะได้ดังนี้
12 = 2 x 2 x 3
15 = 3 x 5
30 = 2 x 3 x 5
ขั้นตอนที่สาม นำเพื่อตัวประกอบร่วมมาคูณกัน และเนื่องจากมีตัวประกอบร่วมเพียงตัวเดียวจะได้
3 = 3
ดังนั้น หรม ของ 8 และ 12 คือ 4
ตัวอย่างที่ 4 จงหา หรม ของ 24, 48 และ 60
เพื่อทำให้คุณเข้าใจมากขึ้น มาดูตัวอย่างการหา หรม ของตัวเลข 3 ตัวอีกสักตัวอย่างกัน
ขั้นตอนแรก แยกตัวประกอบของของ 24, 48 และ 60 จะได้ดังนี้
24 = 2 x 2 x 2 x 3
48 = 2 x 2 x 2 x 2 x 3
60 = 2 x 2 x 3 x 5
ขั้นตอนที่สอง จับคู่ตัวประกอบร่วมของตัวเลขทั้งสามตัวจะได้ดังนี้
24 = 2 x 2 x 2 x 3
48 = 2 x 2 x 2 x 2 x 3
60 = 2 x 2 x 3 x 5
ขั้นตอนที่สาม นำตัวประกอบร่วมที่เหมือนกันมาคูณกัน
2 x 2 x 3 = 8
ดังนั้น หรม ของ 24, 48 และ 60 คือ 8
ตัวอย่างที่ 5 จงหา หรม ของ 6, 18, 24 และ 30
สำหรับตัวอย่างสุดท้าย จะเป็นการหา หรม ของตัวเลขสี่ตัว
ขั้นตอนแรก แยกตัวประกอบของ 6, 18, 24 และ 30 จะได้ดังนี้
6 = 2 x 3
18 = 2 x 3 x 3
24 = 2 x 2 x 2 x 3
30 = 2 x 3 x 5
ขั้นตอนที่สอง จับคู่ตัวประกอบร่วมของตัวเลขทั้งสามตัวจะได้ดังนี้
6 = 2 x 3
18 = 2 x 3 x 3
24 = 2 x 2 x 2 x 3
30 = 2 x 3 x 5
ขั้นตอนที่สาม นำตัวประกอบร่วมที่เหมือนกันมาคูณกัน
2 x 3 = 6
ดังนั้น หรม ของ 6, 18, 24 และ 30 คือ 6
ในบทความนี้ นั่นก็เป็นวิธีการหา หรม ด้วยวิธีการแยกตัวประกอบที่คุณได้เรียนรู้ และสามารถนำไปใช้ประโยชน์กับการเรียนของคุณได้ ถ้าหากคุณมีคำถามหรือข้อสงสัยสามารถถามเราได้ในกล่องแสดงความคิดเห็นได้เลย และเจอกันใหม่ในบทความหน้า